1. Home
  2. 科目別本格的勉強法：数学編

科目別本格的勉強法：数学編

【小学校算数】

　小学校の「算数」の本質は「計算」にありますが、その特徴は「具体性」（目で見て分かりやすい）、「現実性」（身の回りのことに結び付けやすい）、「実利性」（知っていると役に立つ）にあると言えます。
　実際、江戸時代の寺子屋での教育（初等教育）でも「読み」「書き」「そろばん」が3本柱でしたが、前二者がリテラシー（基本的読み書き能力）で、「そろばん」は「計算・勘定」に関わるものですから、生活上欠かせない基本的能力として重視されたということでしょう。今日であれば、小学校2年生で「筆算」と「九九」を覚え、小学校4年生で「小数」「分数」が出て来て、小学校5年で「三角形」「四角形」「円」といった基本図形の面積公式を学び、小学校6年では「立方体」の体積まで扱います。ここで「代数」（数学の中で特に数そのものについて扱う分野）と「幾何」（数学の中で図形について扱う分野）に関する基本的知識、計算方法を学び終えたことになるわけです。
　もちろん、小学校の「算数」でも「発想」は要求され、高学年になるほどその比重とレベルは上がっていきますが、基本的にはあくまで「計算」が主体であり、「発想」といっても理解が困難というレベルではなく、「尺度認識」（目盛りを読む。時間認識をこれに入れてもいいですね）、「単位互換」（km⇔m⇔cm⇔mm、kg⇔g、L⇔dL⇔mL）といった「発想の転換」から始まって、せいぜいクイズ的な「発想の拡張」「逆転の発想」（別な角度から考えてみる。アルキメデスが王様から黄金の王冠がニセモノではないか確かめてほしいと問われて、風呂に入った途端、同じ目方の黄金と王冠をそれぞれ水に入れて、あふれた水の量を比較すればいいと気づいて、「エウレーカ〔我、発見せり〕、エウレーカ！」と叫んだことが思い出されますね）どまりです。

（１）計算力強化
　小学校の「算数」からしてダメだったという人は基本的には「計算力」に問題があったというケースになります（もちろん、小学校レベルでの「発想の転換」「発想の拡張」「逆転の発想」でも最初はなかなか難しいものですが）。端的に言えば「計算スピードが遅い」ということになるでしょう。なぜなら、「基本スキル」である「計算」には「正確さ」と「速さ」という2つの要素が要求されますが、最終的には「計算スピードの中にその人の計算力が表われる」と言っても過言ではないからです。逆に言えば、この段階で十分な訓練が出来ていないと、すなわち計算が遅いままだと、「算数」が苦手なままで放置されている状態ですから、この「計算力」をベースとして、より高度な発想を扱う「数学」の段階に入った時、挫折するのは目に見えているわけです。 そこで対症療法としては、「簡単な計算を何度も繰り返して正確さ・速度を上げる」ということになります。今流行の「100マス計算」もここにスポットを当てているとも言え、こうした「計算」のみならず、「音読」などといった「単純作業」が脳や反射神経に刺激を与え、活性化やボケ防止に効果があることが知られています。実際、小学校の「算数」レベルの「計算」は「時間さえかければ誰でもできる」ものですから、この段階で挫折した思いのある人は思い切って小学校の教科書を買って来て、一通り目を通し（6年分といえども6年かかるわけではありません。わずか数日、数週間で全ておさらいすることはいくらでもできます）、そこに出て来るような簡単な計算問題を次から次へとこなしてくのが結局早道ということになります。実際にこの方法を実践して数学が大得意になったのみならず、その成果は他の科目にも波及して成績が急上昇し、自信がついたためか、スポーツも人間関係も充実して、ついには大学卒業後、大手化学メーカーに就職して副社長にまでなったケースが報告されています（小学校の算数が苦手だった人が理系のトップ・エリートにまでなってしまったということです）。

（２）小学生の3大関門は「小数・分数」「単位互換」「文章題」
　小学校の算数から苦手だった人は、まず「基本ツール」が自分のモノになっているか確認し、「計算スピード」を上げるよう訓練して（「数字慣れ」が必要です）、「小学生の3大関門」とされる「小数・分数」「単位互換」「文章題」に集中的に取り組めば良いということになります。

①算数の「基本ツール」
　九九、筆算、計算のルール（加減よりも乗除が優先、割り算は逆数の掛け算、(　)内が優先、四捨五入など）、面積公式（四角形、三角形、円）、三角形の内角の和、円周率、体積公式（直方体）、倍数・約数、平均、道のり・速さ・時間の公式、グラフなどです。

②小数・分数
　小学4年から学び始めますが、小数・分数を互換したり、小数が入った筆算のルールや分数の通分・約分が分からない子は多いです。

③単位互換
　長さ（mm⇔cm⇔m⇔km）、重さ（mg⇔g⇔kg）、量（mL⇔dL⇔L⇔kL）、広さ（cm⇔m⇔a⇔ha⇔km）、体積（cm⇔m）、時間（日⇔時間⇔分⇔秒）、速さ（時速⇔分速⇔秒速）、割合（％⇔割・分・厘⇔小数）などです。m（ミリ）は千分の一、c（センチ）は百分の一、d（デシ）は十分の一、k（キロ）は千倍を表わすことを知っておくといいですね。

④文章題
　小学1年からでも問題の意味が取れない子はいますが、問題の意味する所を数式に置き換えられない子は小学3～4年から急増します。「食塩水の濃度」「道のり・速さ・時間の関係」「原価・定価・売値の関係」などは小学生が苦手にしやすい典型問題で、中学生・高校生になってもまだ苦手にしている生徒はたくさんいます。

（３）「出来るようになること」が最善の特効薬
　算数が苦手になってくると、「出来ない」→「おもしろくない」→「やらない」という悪循環にはまってきます。こうした生徒への指導で、効果を上げた方法は共通しており、それは「規則正しい生活」と「基礎の徹底」から始まっています。そうすると、「出来るようになる」→「おもしろくなる」→「ほっといてもやるようになる」という好循環が生まれてくるのです。

（４）算数から数学へ
　そもそも「算数」と「数学」の違いは何か、ということが問題になりますが、前者の本質は「計算」（calculation）にあり、後者の本質は「数理」（数的論理、logos）にあることが分かります。教育原理の言葉で言えば、前者の教育は「実質陶冶」（覚えた分だけ利益になる）に相当し、後者の教育は「形式陶冶」（思考のフレームワークを形成する）に相当するとも言えるでしょう。
　もう少し詳しく見ていくと、元々、数学には「計算」と「発想」という2つの要素があるのですが、小学校の算数は「計算」から始まり、高学年になると次第に「発想」が入ってきて、中学校になるとさらに「発想」の比重が高まり、高校以上になると「発想」自体が高度化してくることが分かります。この関係を図示してみましょう。



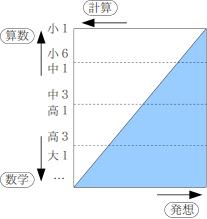
　したがって、小学校での挫折は「計算力」の問題、中学校での挫折は「新しい発想への対応」の問題、高校での挫折は「発想の高度化」の問題と言い換えることができるでしょう。まず、この点を明確にすることが重要なことです。
　例えば、ノーベル物理学賞を受賞したアインシュタインは、ベルリンの市電でおつりの計算を間違えて、車掌から「あなたの欠点は算数ができないことですね」と言われたことがあり、いわゆる計算は「苦手」だったようです。ところが、「自分が光と同じ速さで移動したらどうなるか？」などと突拍子もない「発想」をして、壮大な相対性理論の世界を構築したのです。 　あるいは、現代数学の礎を築いた大数学者ヒルベルトも、その原論文には無数の「計算間違い」があったことは有名です。ところが、こうした細部の誤りにもかかわらず、最終的には正しい結果を導き出しているのです。「直観」と「想像力」でゴールには最初から到達していたのでしょう（アインシュタインも相対性理論の研究に7年もかけていますが、論文自体はわずか5週間で書き上げています。「計算」は「後付」ということですね）。
　さらに「数学の帝王」と称されたドイツの天才数学者ガウスも、小学校の頃、先生から「1から40まで足したらいくらになるか？」という問題を出されて、クラスメート達が四苦八苦しているところに、あっという間に答を出して、相当時間はかかるだろうと思っていた先生をあっと言わせたことは有名です。クラスメート達は順番に1＋2＋3＋4＋･･･と「計算」を一生懸命していたのですが、ガウスは1＋40は41、2＋39も41、3＋38も41、これが20個できるので、41×20＝820と「発想」したのです。つまり、クラスメート達は「算数」をしていたのに対し、ガウス1人は「数学」をやっていたわけですね（これは幾何的には平行四辺形の面積と同じで、代数的には三角数の和、数列的には等差数列の和として考えます）。

【中学校数学】

　中学校の数学になると、文字x, yを使ったり、π（パイ）だのrだのを使って「公式の記号化」が出てきたりします。つまり、中学校の「数学」の特徴は「抽象性」（現実性、実利性が薄れていく）、「一般性」（個別性を離れていく）、「汎用性」（いろいろなケースに応用することができる）を帯びてくることにあると言ってもよいでしょう。つまり、中学校の「数学」では「発想」の部分で「抽象化」が起きてくるわけです。
　ここで、「計算」が得意な子でも行き詰るケースが出て来ます。例えば、そろばんが得意で暗算はすごくできるのに、数学の問題を解くのは苦手という場合がありますが、これは「新しい発想」になじみきれないために起きて来ます。つまり、新たに「抽象的思考」が要求されるために生じる現象です。中学校の数学では「数の概念」が拡大され、「負の数」や「無理数」が出て来て、そろばんで扱っているような「現実的な数」（これは「自然数」の世界です）を超えてくるわけです。
　あるいは、計算問題はできても、文章問題になると弱いというケースもありますが、これは「文意」の中にある「数的論理」（結局、何が問題とされているか）や「数的連関」（結局、何を求めれば解答に至るか）をつかめていないために起こります（「数理による再構成」ができないということです）。大体、国語・英語・数学といった基本教科において、要求されている力は「論理的思考力」にあると言えますから、「基礎的知識」（国語なら漢字・文法、英語なら単語・熟語・文法、数学なら基本公式）を覚える段階を超えれば、「本質」は一緒になります。試験でも「どう思うか」といった人の数だけ答があるような「主観的感性」を問う問題は出すことが出来ず（そもそも「内面の自由」は絶対的自由権ですから、それについてあれこれ評価することはできません。どうしてもこうした人間性の部分を見たければ「面接」「小論文」といった「人物評価」の試験形式にするしかないのです）、「何のテーマに関して、何を根拠に、どこまで論じられているか」「1なる解答にどこまで到達できているか」といった「客観的思考力」のみが「能力の差」として問われるわけです（そもそも試験は「入学させるため」に行われるのではなく、「落とすため」に行われるものです。何たって「定員」があるわけですから）。
　では、「計算」の進展と共に生じた「数の概念」の拡大（「より上位の包括的概念」が現われ、いわゆる「パラダイム・シフト」が起きていることが分かります）という観点から、中学校数学の位置付けをしてみましょう。端的に言えば、次のようになります。

数の概念 扱う数学
自然数、整数 小学校低学年の算数
有理数 小学校高学年の算数（特に小学校4年以上）
実数 中学校の数学（特に中学校3年以上）
複素数 高校以上の数学（特に高校2年以上）

①自然数（natural number）
　元々、「数」（number）は「数える」（count）という動作・行為と不可分な関係にありますから、数の出発点は1, 2, 3, ･･･といった「個数」や「順序」を表わす「自然数」になります。ただ、民族によって、区別しているのは「1」「2」「多」だけであったり、「100以上」を表わす概念は無かったりするわけです。対応しているのは小学校低学年の算数です。

②整数（integral number）
　ところが、自然数だけだと「引き算」で無理が生じてきます。「ある数」から「同じ数」を引けば「0」になってしまいますし、「より大きな数」を引けば「負の数」が出て来るからです。実際、現実生活における「数える」という行為の中だけでは、「0を3個持ってきて」とか「バナナを－3本ちょうだい」などということはあり得ないわけです。そこで、「0」（これはインドで発見され、アラビアでこの表記を得ました）と「負の数」（negative number、これも商取引などの必要性からインドで発見されました）を加えて、「整数」なる概念が現われ、従来の「自然数」はその中の「正の数」（positive number）であると認識されるようになりました。そして、ここから「数直線」（number line）が登場してくるわけです。これも小学校低学年（「負の数」の計算そのものは中学校1年で学びます）の算数に相当します。

③有理数（rational number）
　「整数」の計算では「割り算」の時に無理が生じます。「割り切れる数」だけでなく、「割り切れない数」が出て来るからです。そこで、次のような形で表わされる「有理数」の概念が登場しました。
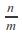（n, mは整数、m≠0）
　「ratio」とは「比」のことですから、「整数の比で表わされる数」ということになりましょう。「有理数」の中では「分数」（fraction, broken number）が比較的早く発見され、それから大分遅れて「小数」（decimal fraction）が発見されました。特に「小数」は「有限小数」（0.5, 1.75など、terminating decimal）と「無限小数」（infinite decimal）がありますが、「有限小数」及び「無限小数」の中の「循環小数」（0.333･･･など、recurring decimal）のみが「有理数」に属します。「小数」「分数」は小学校4年から学びますので、これは小学校高学年の算数の世界であると言えましょう。
　ここで問題を1つ出してみましょう。
【問題】循環小数0.12121212･･･を分数の形に直せ。
【発想】循環小数は有理数ですから、必ず分数表記されるはずですが、無限に続くものをどうやって扱うの？といったところですね。これは両辺を100倍して元の式を引いて「無限」を消せばいいと「発想」するのです。
　x＝0.12121212･･･　　･･･①　両辺を100倍すると･･･
　100x＝12.121212･･･　･･･②　②から①を引くと･･･
　99x＝12　　　　　　　アラ、不思議、「無限」が消えました！
　∴x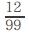＝　　　　となるわけです。
　これと同じ発想を等比数列の和（等比級数）でも使います。実に数学の歴史の中で、こうした「すぐれもののアイデア」（この場合、無限に続く小数を無限に計算しなくても、単純な掛け算と引き算だけで消去してしまう）があちこちにちりばめられており、これを普通は単純に「受験テクニック」として学んでいくわけですが、まずもって「アイデアのすばらしさ」そのものに「感動」する「心、感性」の方が重要だと言えるでしょう（無味乾燥な「公式」をひたすら覚え込むより、「頭いいなー、コイツやるな！」「誰がこんなこと考えたんだろう？」などと考え、感じながら、アイデアそのものを自分のモノにしていく方が楽しいに決まっていますね）。

④実数（real number）
　「小数」の中で「有理数」の範囲に収まらないもの、それが「循環しない無限小数」ですが、これを「無理数」（irrational number）と言います。そして、「有理数」と「無理数」を合わせて「実数」という概念が生まれて来ました。こうして見ると、何だか「有理数」には「道理」があって、「無理数」には「無理」があるかのようですが、「比で表わされる数」「比では表わされない数」ということですから、「有比数」「無比数」と言ってもいいぐらいでしょう。この「無理数」の存在自体は測量・図形といった「幾何」の計算で出て来るので、古代エジプト・ギリシアの時代から知られていました。
　例えば、有名な「ピタゴラスの定理」（三平方の定理、直角三角形の斜辺の2乗は他の2辺の2乗の和に等しい）でも、直角二等辺三角形の場合、三辺の比は1：1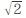：（ルート2、2乗すると2になる数）になるわけです（もっとも宗教的秘密結社であったピタゴラス教団においては、「無理数」はタブーであり、その存在をもらした者には死が待っていたと言います）。あるいは「円」において、「円周」を「直径」で割れば「円周率」π（パイ）が出ますが、これも「超越数」（いわゆる「方程式」〔正確に言うと整係数の代数方程式〕の解にならない実数、代数的数でない実数、transcendental number）と呼ばれる「無理数」です。これは円を扱う上で欠かせない数字と言えますが、そもそも図形の中で最も基本的なものは「円」（曲線図形の中の最単純形で、周囲が同じ長さの図形の中で面積は最大となる）と「三角形」（直線図形の中の最小角形であり、他の直線図形は全て三角形の和から成る）ですから、「測量術」から発達した「幾何学」でもこうした「無理数」を「数の体系」の中に組み込まざるを得なかったのです。かくして「実数」なる概念が打ち出され、「現実的な数」が全て網羅され、「数直線」は「連続体」として完結しました。
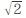＝1.41421356･･･（一夜〔ひとよ〕一夜に人見頃〔ひとみごろ〕･･･）
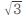＝1.7320508･･･（人並みにおごれや･･･）
e（「自然対数の底」と呼ばれる「超越数」です。超重要な数なので、高校3年の数Ⅲで学びます）＝2.718281828･･･（鮒〔ふな〕一鉢二鉢一鉢二鉢･･･）
π（パイ）＝3.141592653589793・・・（身一つ世一つ生（い）くに無意味、いわく泣く身・・・）
　こうした「無理数」を本格的に学び始めるのは中学校3年からですから、「実数」は中学校数学の世界であると言ってもよいでしょう。

⑤複素数
　「未知数」を求める際に「方程式」（equation）を用いますが、「未知数」（「変数」〔variable〕とも言います）xの1次式を使って問題を解くことを「1次方程式（linear equation）を解く」と言い（方程式を成り立たせる文字の値を「解」（solution）と言います）、一般的には次のように表わされます。
ax＋b＝0（a, bは実数、a≠0）　∴x＝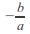
　さらに未知数が2つ以上あれば、「連立方程式（simultaneous equation）をつくる」ことになります。例えばx, yの2つの未知数（「元」〔げん、element, member〕とも言います）を使った連立方程式は「2元連立方程式」（simultaneous equation with two unknowns）と言います。小学校で紹介されたりするいわゆる「鶴亀算」（「鶴と亀が合わせて7つ、足は合わせて22本、さて鶴は何羽、亀は何匹？」といった問題ですが、「そんなの見たら分かるじゃん！」という根強い批判もある計算です）などもここで「抽象化」「一般化」されます（例：x＋y＝7、2x＋4y＝22の連立方程式を解く）。基本的に未知数の数だけ連立方程式があれば、「解」を求めることができるということは知っておくとよいでしょう。
　そして、2次方程式の「計算」の段階に至った時、「実数」の範囲に収まらない数が出て来たのです。一般的に2次方程式は次のように表わされます。
　ax2＋bx＋c＝0（a, b, cは実数、a≠0））　x＝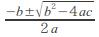
　2次方程式自体は中学校3年で学びますが、「一般解」を求めるこの「解の公式」（インドで7世紀頃に発見されました）は高校1年の数Ⅰで学びます。ここでのルートの中のb2－4acが「正の数」「0」ならxは「実数解」となりますが、「負の数」の場合が困るのです。そこでb2－4acを「判別式D」と名付け、「解が2つ」「解が1つ」「解なし」の3つのパターンの見極めのポイントとされました。数Ⅰではこれをグラフと結び付けて学び、「代数」と「幾何」を「座標平面」という統一された場で扱います。ちなみにこれはデカルトが発明した革命的アイデアで、「デカルト座標」「直交座標」とも言います。なぜなら「代数」という「数」の問題を「幾何」的に目で見て考えることができるようになったからです。別物と思われていたものが、実は「同じ物の別表現」であることが分かったわけです。
　ところで、2次方程式の「解の公式」を突き詰めていくと、やはり2乗すると「負の数」になるような数の存在を想定せざるを得ません。そこで「虚数」（imaginary number）なる「概念」が出され、2乗すると－1になる数を「虚数単位i」（i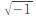＝、i2＝－1。なぜ2乗するとー2になる数でもなく、－3になる数でもないかというと、これらは全て虚数単位の実数倍で表現されてしまうので、虚数単位さえ設定してあればいいからです）と名付け、「実数」と「虚数」を合わせた「複素数」（complex number）なる「数の概念」が出て来たのです。ただし、「虚数」といっても、これはあくまで「実」（現実的数量として把握できる数）に対する「虚」（現実的数量ではないが、数学的実在として想定できる数。いわゆる「霊的世界」などもこの虚数の観点で説明できるのではないか、と考察を試みるニューサイエンティストもいます）であって、決して「空しい、空虚な数」ということではありません。「複素数」は一般的に次のように表現されます。
a＋bi（a, bは実数）
　つまり、従来の「実数」は「複素数」の中の「虚部」がゼロ（b＝0）の数（「実部」のみ）の数であることが分かったのです。これは高校2年の数Ⅱで初めて学び、大学で本格的に学ぶ内容ですので、高校数学以上の世界（特に高校2年以上）であると言えるでしょう。したがって、これを学ばずして、数学のフィールドを自由に行き来することは出来ないと言っても過言ではないのです（というより、これを知らないとはっきり言ってソンです！ああ、もったいない、もったいない）。
　さて、話が高校数学のレベルを超えて進んでしまいましたが、ここで中学校数学が苦手な場合の対症療法です。改めて整理すると、中学校数学で挫折するのは次の2パターンということになります。

①小学校時代から「計算スピード」が遅く、苦手を引きずっていた。
②新たに出て来た「抽象的思考」に対応し切れなかった。

　①の場合は「計算のやり直し、スピードアップ化」が有効ですが、②の場合は有効なのが「証明問題」です。丸暗記型の人間なら、証明の結果、得られたものを公式として丸覚えするところですが、「どうしてそうなるのか」という「証明」を自ら「追認」（物理なら「追実験」となります）することで、その「数的論理」を自分のモノにする必要があるわけです。そもそも中学校数学のレベルは、数学史で言えば大体1600年代前半までのレベル（デカルト）であり、高校数学・物理のレベルは大体1600年代後半から1700年代前半のレベル（ライプニッツ、ニュートン）です。さらに1700年代後半以降の数学（オイラー、ガウス）は大学レベルと言ってもいいでしょう。だんだん丸暗記で対処できなくなってくるのは一目瞭然です。したがって、先人達の発想をより洗練されたエレガントな方法で効率よく吸収していくのが数学の勉強であると言ってもよく（シュプランガーの文化教育学の観点で言えば、「数学教育」ほど、典型的な「人類の歴史的遺産の相続」はないと言えるでしょう）、本来なら天才でないと思いつかないようなアイデアの数々を現代人であるということだけで、中学、高校ですでに自分のモノにできるという「時代的恩恵」をむしろかみしめるべきではないでしょうか（実はすごいことを勉強しているんです。まあ、今は小学生でもパソコンやケータイを使いこなし、ゲーム機器も驚くほどのハイテクですから、昔の人から見れば信じられないことでしょう）。実際、ドラえもんのタイムマシンに乗って、今の中学生、高校生が1600年代、1700年代に行けば、きっと天才扱いされることでしょう（例えば、ニュートンの講義は難しすぎて聴く人がいなかったと言います。ところが、今の高校生で理系の子なら「何だ、これ、微分じゃん！」「万有引力のことでしょう？4つの力のうちの1つなんだよね。」と感想をもらすかもしれません）。

【高校数学】

　高校の数学になると、いわゆる学問としての数学の基礎としての「概念」が出て来ます。それも1年生段階ですと「基礎の基礎」であり、中学校数学の延長で対応することもできますが、2年生以上レベルになると複素数・ベクトル・行列・微分・積分など、日常的に使う人がごく限られる「基礎概念」を学ぶので、「一体何のためにこれを学んでいるのか」「公式を当てはめて答は出るけど、意味が分からない」という苦しい状況に追い込まれることになります。しかし、逆にこうした基礎概念抜きに、その先に待っている「数学の豊穣なる世界」を理解することはできません。実際、ここまでくると、現実との直接的つながりはほぼ断ち切られ、まさに「数学の数学たる所以」の世界に突入すると言ってもいいでしょう。いくら2次関数の放物線は弾丸の軌道とか、サイン・コサイン・タンジェントといった三角比は測量で使うとか言われても、ほとんどの人の現実生活、日常生活とは無縁のものでしょう。あるいは確率とか微分は経済学でも必要、理系に進んでコンデンサーを学ぶ上で複素関数は不可欠であるとしても、一般ピープルにベクトルの内積や行列計算など「我に何の関わりあらんや」と言いたくなるところです。
　実は数学とは「抽象論理」そのもので、応用数学の世界の代表が物理の世界です（さらに数学の導入で成功した物理学に倣ったのが経済学の世界です）。「算数」の段階では苦手ではあっても「やればできる」と言えますが、数学の本来的フィールドではいくつかの条件を満たさないかぎり、「やってもできない」ということになってきます。その前提条件の1つが「抽象論理」としての「概念」を駆使できるかどうかにあるのです。この「抽象化」は数学に限らず、全ての近代学問の特徴でもあり、合理主義の行き着いた地点として爆発的な影響力を持ちました。例えば、経済学におけるモデル・ビルディングなどもそうですし、経済の根幹にある「契約」が「抽象化」されておらず、相手との人間関係（血縁、コネ、賄賂など）によって左右されるような個別性があるようであれば、近代的市場も近代資本主義も成立しないことが明らかになっています（「近代的所有権とは抽象的・絶対的・直和的〔誰に属するかが一義的に決まる〕でなければならない」と表現されます）。

（１）「定義」の確認と「公式」の理解・暗記は全ての基本
　「定義」＝用語について、その意味内容を正確に定めること、または定めた意味。数学はここから出発して、巨大な体系・世界を構築しています。定義とはいわば根本原理であり、あらゆる性質（定理や公式）はこの定義から論理的に導かれなくてはいけません。数学は「論理」を最も大切にする学問であり、その「論理」は誰に対しても同じ結論に導くものでなければならないので、そのためにはまず用語や記号の意味が明確でなければならず、それ故、数学は定義にうるさくなるのです。
「公理」＝定義から何の前提もなく、正しいと分かる事柄。全ての議論の前提となる最も基本的な仮定。数学という学問としては、こうした証明なしに採用される数少ない基本仮定を出発点に置き、それらの公理だけから厳密な演繹（論理の展開）によって全ての結果を導き出す構造にしたいわけです。
「定理」＝定義と公理から、第三者が理解できないようなジャンプをせずに説明できる事柄。定理を数式で表わすと、「公式」となります。例）三平方の定理、正弦定理、余弦定理など。
「公式」＝証明されたものですから、誰がやっても同じ結果となります。変数を使って一般的に表記してありますが、そこに具体的数値を入れていけば答えが自動的に出るわけですから、計算の手間を省く便利な道具だと考えるべきです。したがって、どれくらいの公式を使いこなせるかは用途に応じた道具立てということになりますので、充実していればいるほど対応力が増すことは当然のことです。

（２）「設問」読解と｢条件｣の数式化がカギ
　「設問」読解の意義＝実は「数学力」「解答力」は「問題が要求しているものを読み取る力」（一般的に言えば、「問題点の明確化」）と「そのためには何が分かる必要があるか（何が分かりさえすればいいか）を見抜く力」（一般的に言えば、「解決の筋道の明確化」）と言ってよいでしょう。「定理」や「公式」を使おうにも、そもそもそれらは「道具」ですので、「何のために使うのか」という「目的」が明確でないと使いようがないのです。
　「質問」の意義＝学習を進めていく上で、「質問」は不可欠ですが、実は「質問の仕方」にもコツがあり、こうした「問題点の明確化」「解決の筋道の明確化」を徹底的に追求した上で成される質問は、解答・解法・解説に接した時に格段の理解力をもたらすものです。これをいわゆる「良い質問」と言います。こうした「これを求めるためにここさえ分かればいいのに、ここがどうしても分からない」といった詰めの作業（当然、調べたり、考えたりする作業を伴う）をせずに、ただ何となくその都度成される質問は「ただの質問」であり、熱心に勉強し、質問も多いのに、なかなか伸びないという場合はこうした「質問の仕方」を再検証する必要があります。相対性理論を確立し、ノーベル物理学賞を受賞したアインシュタインも、「もし私が1時間後に殺されるとしたら、最初の55分間は適切な質問を考えることに費やすだろう」と言っています。
　「条件」の数式化＝問題によっては「何を求めればいいか」は分かるものの、「そのためには何が分かりさえすればいいか」が分かりにくい場合があります。この時は、与えられた条件を整理して、数式で表現しておく作業が活路を開くことが多いものです（これは0≦x＜3といった「定義域」の確認等でも必要な作業です）。「何が分かりさえすればいいか」という発想は「演繹的」（論理的必然性）ですが、「条件を整理していくうちに道が見えた」という解決の仕方は「帰納的」（現実的妥当性）であり、こちらがダメならあちらでどうか？と考えるべきものです。
　「図式化」による視覚化＝一般的に問題文に書いてある内容をまず図や数式で表わし、一目瞭然の形にするのが効果的・効率的です。頭の中だけで論理的に考えようとすると、よほどワーキングメモリ（超短期記憶装置）が強力な人でない限り、なかなか進まないものですが、図式化・視覚化して「目で考える」ようにすると誰にでも処理しやすくなるのです（この手法は新人アナウンサーの研修などでも使われています）。

（３）「パターン」（文系的ゴリゴリ）と「センス」（理系的キレイ）の違い
　「パターン」攻略＝「公式」をただ覚えるだけでは難しい応用問題はなかなか解けませんが、問題特有の「パターン」を知っていれば、応用力・解答力が格段についてきます。これは英語で言えば、「文法」→「構文」→「読解」のうちの「構文」に相当するものであり、数学ではこれが「公式」→「パターン」→「解法」となるわけです。「要は解ければいいんでしょ」というのが文系の基本的スタンスなので、必須・頻出「パターン」をなるべく多くモノにすることが数学力アップに直結します。
　数学的「センス」＝解法の中には「うわ、スゴイ！」「よくこんなアイデア思いついたな」などとうならせるものがありますが、これは典型的な「センス」（数学的感性）と言えるでしょう。同じ解くにしても「よりエレガントに解く」ことに美しさを感じるわけです。理系は基本的に自然科学者の卵と言ってもいい所があり、これは「科学者の基本的感性・特性」と言ってもいいかもしれません（「数式は美しくなければならない」という信念を持っている人は多いのです）。
　「怠け者の発想」＝受験ではあくまでも「答えがある問題」を扱いますので（「答えがあるか無いか」というような「存在問題」は難問すぎるのです。ましてや「新しい法則を発見せよ」といった問題はまず出ません）、「1なる答えに至る筋道」が「うまく」確保されればいいのです。理系的発想には「なるべくラクをしたい」というものもあり、ここから「基本原理の理解とショートカットの駆使」という手法が生まれてくるのです。

（４）「場合分け」と「論理」の2大ツールを駆使する
　「場合分け」＝「論理の筋道」を明確にするため、「考え得る場合を全て数え上げる」ことが有効です。これは「思考の漏れ」を無くすための方法ですが、「数学」は本来「数の学問」「数えることから始まった学問」なので、「数学の本質」に即した考え方とも言えます。
　「論理」の力＝「数学」を「自然科学の女王」たらしめ、「近代化」の覇権をもたらしたのも、この「論理」の力（思想的に言えば「合理主義」）に他なりません。これは「こうでもあるし、ああでもあり得る」といったあいまいさを残すものではなく、「これ以外にあり得ない」「こうであるはずだ」という「一義的決定」「必然性の思考」であり（人の数だけ答えがある「主観主義」ではなく、誰が見ても1つの答えに定まる「客観主義」です）、これに気が付けばあらゆる勉強・学問の根本は一緒だということが理解され、数学のみならず、英語も国語も全ての学力が急激に伸びてくるのです。

（５）高校数学から大学数学へ
　高校数学で不可欠な「抽象的概念」を理解するためのコツは、次の2つになります。

①ビジュアル化する。
②数学の全体系の中で位置付け・意味付けをする。

　①はなるべくグラフや図形に表わすようにして、「目で考える」ということです。これは「抽象化」のゆえに理解が困難になってくるからで、ならば「具体化」すればいいということになるわけですが、すでに「現実性」を遠く離れているので、せいぜい「視覚化」すること止まりとなるわけです。しかし、アインシュタインをはじめとして、天才と呼ばれる人達はイマジネーションが豊かで、計算式で考えるよりもビジュアル・イメージが先行し、あとから計算して理論化すると言われますから、有効な方法であることは間違いありません。「虚数」なる現実世界に見出し難いものを座標化（ガウス平面）して扱いやすくしたガウスや、さらにそれを立体の球（リーマン球）で表現して全く新しい意味付けをしたリーマンなど、「イメージの天才」としか言いようがありません。日本で最初のフィールズ・メダリスト（フィールズ賞は「数学のノーベル賞」ですが、その難しさはノーベル賞以上であり、日本人で受賞したのは東大の小平邦彦氏、京大の広中平祐氏、森重文氏の3人だけです）となった小平邦彦氏も「数学を理解するということは、実在する数学的現象を〝見る〟ことである。〝見る〟というのは数覚によって知覚することである」と述べています。
　②は「高校数学の意義付けは中学校数学の延長上ではできない」ということです。なぜ、高校数学でこういった内容を学ぶのか、といった必然性はもっと上の数学の要請から来るわけです。すなわち、大学での数学（高等数学、数学という学問）からの視点に立たない限り、高校数学の意義は理解できないのです。「何のためにこれを学ばないといけないのか」という疑問は「数学の壁」として必ずぶつかるものですが、それは現実的必要性から解決されるのではなく（現実に知っておくと役に立つからではないということです）、「数学的必然性」から克服されるのです。すなわち、「より上の視点から見下ろさなければ今やっていることの意味・意義は理解できない」ということです。
　例えば、「人類の至宝」とまで称えられる「オイラーの公式」（このたった1つの法則を説明するためだけに数百ページもの本が書かれたりしています）を学ぶと、それまで全く別物と思われていた複素関数、指数・対数関数、三角関数が直結し、1つの公式に流れ込んでいく様を見て取ることが出来ます。実際、虚数の意味・意義を考えつつ、複素数のフィールドをさまよっていると、このオイラーの公式に出くわした時、「衝撃」を受けるものです。式にすると「eiπ＝cosθ＋ⅰsinθ」（といきなり言われても、訳が分かりませんね）という至ってシンプルなものですが、θ＝π（パイ）の時、「eiπ＝－1」という驚くべき形を取るのです。「超越数e」を「虚数i」乗し、さらに「超越数π（パイ）」乗すると、何と「実数－1」となるというのです（高校で数学ができる人なら、たいてい「iのi乗はいくらだ？」という問題を出されて、「？」となったことがあるでしょう。虚数の虚数乗なんて全くイメージできないところですが、実はこれ、実数になるのです。正確な数値は電卓が無いと計算できませんが、これが実数になることはオイラーの公式を使えば簡単に理解できます）。見方を変えれば、「全ての数を生み出す根源的な公式」（大体、あらゆる数〔複素数〕を形成する「基本的な数」は「1」「－1」「e」「π〔パイ〕」「i」の5つと言ってもいいでしょう）を「オイラーの公式」に見ることができると言ってもいいかもしれません。これで扱えない数は「0」と「無限」だけと言ってもいいのです（これに対してリーマンは「リーマン球」を使って、「0」と「無限」まで「イメージ」の中に取り込みました）。ところが、高校ではここまで学ばないので、バラバラの知識をバラバラに覚えていくだけなのです。何ということでしょうか。
　こうして見ると、高校まで数学が得意だった人（だから理系大学に進学するわけですが）が大学に入って、数学が全然分からなくなるケースがあることも理解されます。そもそも受験エリートなるものは「解答」がある「問題」を解いて来ただけで（そもそも「解があるかどうか」ということ自体が、「存在問題」と呼ばれる大変な問題なのです）、「数学の体系的理解」をしてきたわけでは必ずしもないのです。したがって、皮肉なことですが、高校数学は本来大学受験を目的とするのではなく、大学数学を目的とし、大学数学の視点から教育されるべきとなります。これに対して、大学受験予備校では受験対策としての技術的知識を教えるのは当然となりますが、現実には今の高校でこうした技術的知識が重宝され（予備校のノウハウを吸収しようという試みが活発になってきました）、学問的視点がほとんど無いことは残念な限りです。まあ、学習指導要領に沿って授業をしなければならないので、現場の先生にこれを要求するのは酷な話ですが。

【大学・社会人数学】

　参考までに数学の体系をざっと見ておきましょう（まあ、何と難しい名前が並んでいることですね。適当にふんふんと読み飛ばして下さい）。

①数学基礎論～論理学、集合論、自然数論など。
　「集合論」は決定的に重要です。また、「必要・十分条件」を知ると、論理の幅が出てきます。「無限論」なども魅力的ですね～。ここは文系向きです。

②代数学～線形代数学、抽象代数学、整数論、ブール代数、群論など。
　いわゆる「数」について扱う所です。少なくとも「複素数」は数の最大包括概念ですから、駆使できるようにしたいところです。

③解析学～位相解析、微分方程式、速度、変分法、複素関数、級数など。
　数学の歴史を大きく発展させていったのはやはり「微分・積分」でしょう。「微（かす）かに分かる、分かった積（つ）もり」などとよく言われますが、これ抜きに物理はなく、経済学における「限界革命」もありませんでした。

④幾何学～角法、ユークリッド幾何学、非ユークリッド幾何学、解析幾何、射影幾何、代数幾何、微分幾何など。
　中学・高校で学ぶ図形問題は「ユークリッド幾何学」で、「初等幾何学」とも呼ばれます。これに対して、19世紀にロバチェフスキーが切り開いた新しい幾何学が「非ユークリッド幾何学」で、アインシュタインの相対性理論もこの恩恵を受けています。

⑤トポロジー～位相空間、次元、多様体、PLトポロジー、グラフ理論、結び目、不動点定理、カタストロフィ理論など。
　幾何学を「変換」という観点で統合（クラインのエルランゲン・プログラム）した上で、特に量が変わらないものを扱い、「粘土の幾何学」「ゴム板の幾何学」と呼ばれます。元々はガウスに並ぶ「万能の天才」オイラー（大体、この2人は数学史上、東西横綱に位置付けられます）の「一筆（ひとふで）書き」の研究から始まりました。

⑥応用数学～確率論、統計学、サイバネティクス、情報理論、ゲーム理論、大数の法則、組み合わせ理論、オペレーション・リサーチなど。
　「確率論」は量子力学や経済学におけるリスク研究を決定的に推進しました。「ゲーム理論」は天才ノイマンの発明です。「大数の法則」は保険などでも利用されているもので、個々人はそれぞれ生活を送っているのに、毎年、一定の割合で事故や病気で死亡するのですから、何だか不思議な気がします（こうした「ミクロ」「マクロ」の視点は実に幅広く応用されています）。

Copyright © 「やる気」が出る勉強法研究会 All Rights Reserved